Indoor Navigation of Quadrotor UAV

Dissertation with distinction

  • Author: Suhang Xia
  • Supervisor: Yunpu Song
  • Affiliation: Department of Mechanical and Automotive Engineering, Zhejiang College of Tongji University
  • Title: Research on Indoor Navigation of Quadrotor UAV

Table of Contents

  1. Simulation Platform Construction and Mathematical Modeling
  2. Design 1: PD Feedforward Compensation Controller for Quadrotor UAV in MATLAB
  3. Design 2: A* Algorithm and Trajectory Optimization
  4. EGO-Planner Algorithm Research
  5. Conclusion and Experimental Results
  6. Acknowledgments

Simulation Platform Construction and Mathematical Modeling

Simulation Platform Construction

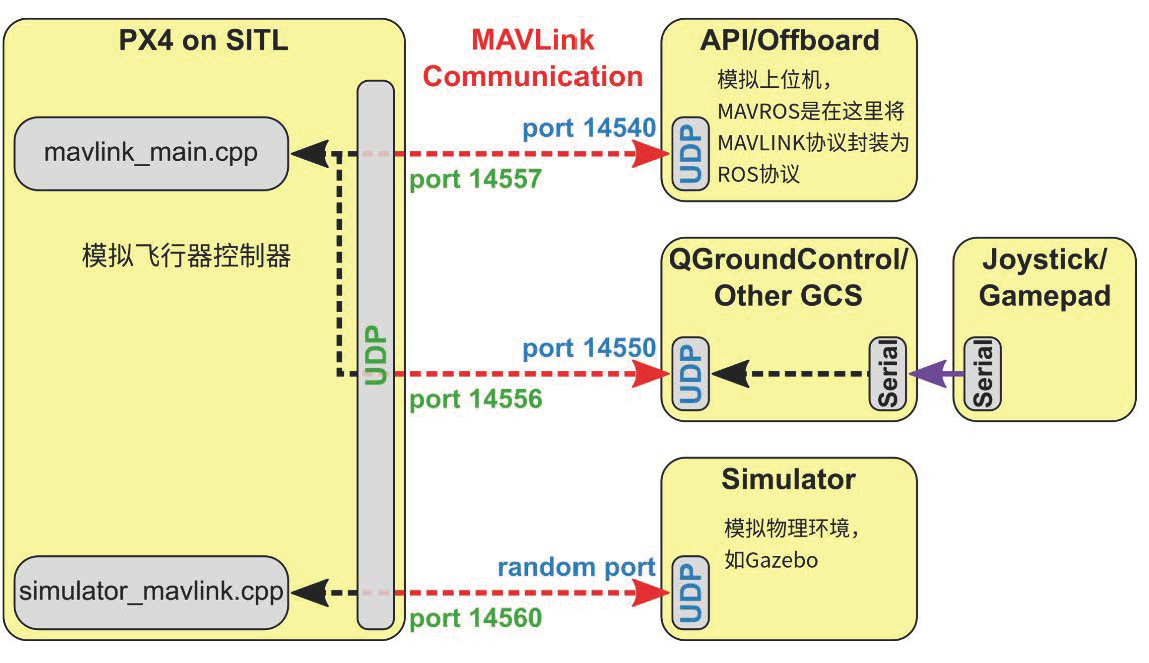
  • Core Components: The simulation platform is constructed using ROS, Gazebo, the PX4-autopilot flight controller, QGC ground control software, and the EGO-Planner algorithm for UAV trajectory planning.

  • Challenges: Conventional simulator maps typically fail to accurately represent real-world conditions, leading to significant discrepancies between virtual simulations and real-life scenarios.

  • Proposed Solution:

To address this critical issue, this study proposes an advanced high-fidelity simulation environment based on LiDAR 3D reconstruction technology. This cutting-edge approach leverages high-resolution LiDAR sensors to capture comprehensive environmental data from real-world scenarios. Through sophisticated spatial reconstruction algorithms, the simulation platform generates highly accurate 3D models that reflect the complexity and dynamic nature of real environments. The constructed platform not only replicates intricate geometric structures but also supports dynamic updates, ensuring that it can faithfully simulate real-world conditions. This unprecedented level of fidelity provides a robust framework for testing and validating UAV autonomous navigation and obstacle avoidance algorithms, offering real-time control feedback. By bridging the gap between virtual and physical testing environments, this innovative platform sets a new standard for high-precision simulations in UAV autonomous driving technology.

UAV Mathematical Modeling

The quadrotor UAV dynamics model is described as follows:

\[\begin{aligned} &\ddot{y}=\frac{U_1}{m}[\cos\varphi\sin\theta\cos\psi+\sin\varphi\sin\psi]-\frac{K_x\dot{x}}{m} \\ &\ddot{y}=\frac{U_1}{m}[\cos\varphi\sin\theta\sin\psi-\sin\varphi\cos\psi]-\frac{K_y\dot{y}}{m} \\ &\ddot{z}=\frac{U_1}{m}\cos\varphi\cos\theta-g-\frac{k_z\dot{z}}{m} \\ &\dot{\phi}=\frac{(I_y-I_z)}{I_x}\dot{\theta}\dot{\psi}-\frac{I_p}{I_x}\dot{\theta}\Omega+\frac{U_2}{I_x}-\frac{K_\varphi p}{I_x} \\ &\ddot{\theta}=\frac{(I_z-I_x)}{I_y}\dot{\varphi}\dot{\psi}-\frac{J_{Ap}}{I_y}\dot{\phi}\Omega+\frac{U_3}{I_y}-\frac{k_\theta q}{I_y} \\ &\ddot{\psi}=\frac{(I_x-I_y)}{I_z}\dot{\varphi}\dot{\theta}+\frac{U_4}{I_z}-\frac{k_\psi r}{I_z} \end{aligned}\]

Design 1: PD Feedforward Compensation Controller for Quadrotor UAV in MATLAB

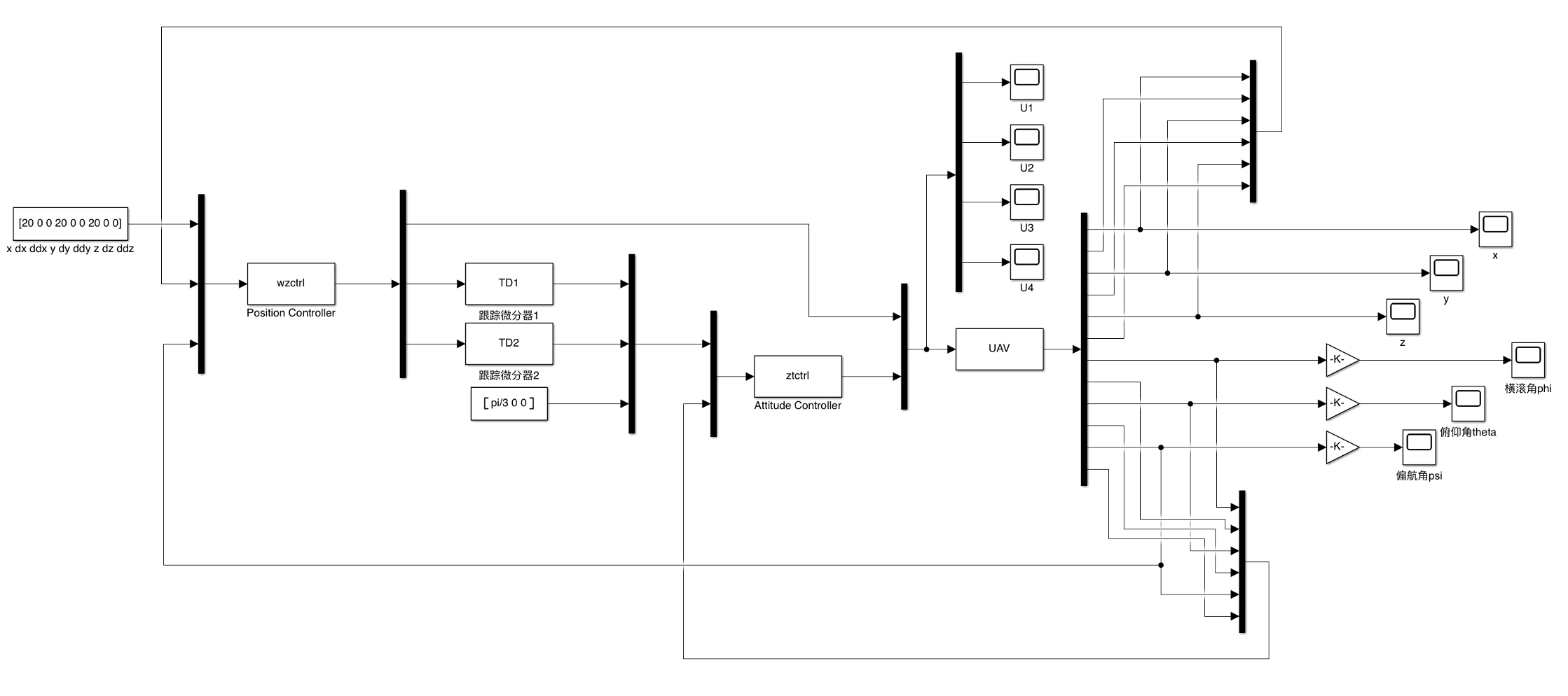
  • Tools: MATLAB-Simulink
  • Inner Loop Attitude Controller: \(u_2\): roll torque, \(u_3\): pitch torque, \(u_4\): yaw torque

\(\begin{align} u_2 &= -k_{p\phi}\phi_c - k_{d\phi}\dot{\phi}_c + \ddot{\phi}_d + \frac{lK_4}{I_x}\dot{\phi} \end{align}\) \(\begin{align} u_3=-k_{p\theta}\theta_c-k_{d\theta}\dot{\theta}_c+\ddot{\theta}_d+\frac{lK_5}{I_y}\dot{\theta}_d \end{align}\) \(\begin{align} u_4=-k_{p\varphi}\varphi_c-k_{d\varphi}\dot{\varphi}_c+\ddot{\varphi}_d+\frac{lK_6}{I_z}\dot{\varphi}_d \end{align}\)

  • Outer Loop Position Controller: \(u_1\): vertical thrust \(\begin{align} u_{1x} = -k_{px}X_c - k_{dx}\dot{X}_c \end{align}\) \(\begin{align} u_{1y}=-k_{py}Y_c-k_{dy}\dot{Y}_c \end{align}\) \(\begin{align} u_{1z}=-k_{pz}z_c-k_{dx}\dot{Z}_c+g+\ddot{Z}_c+\frac{K_3}m\dot{Z}_c \end{align}\)

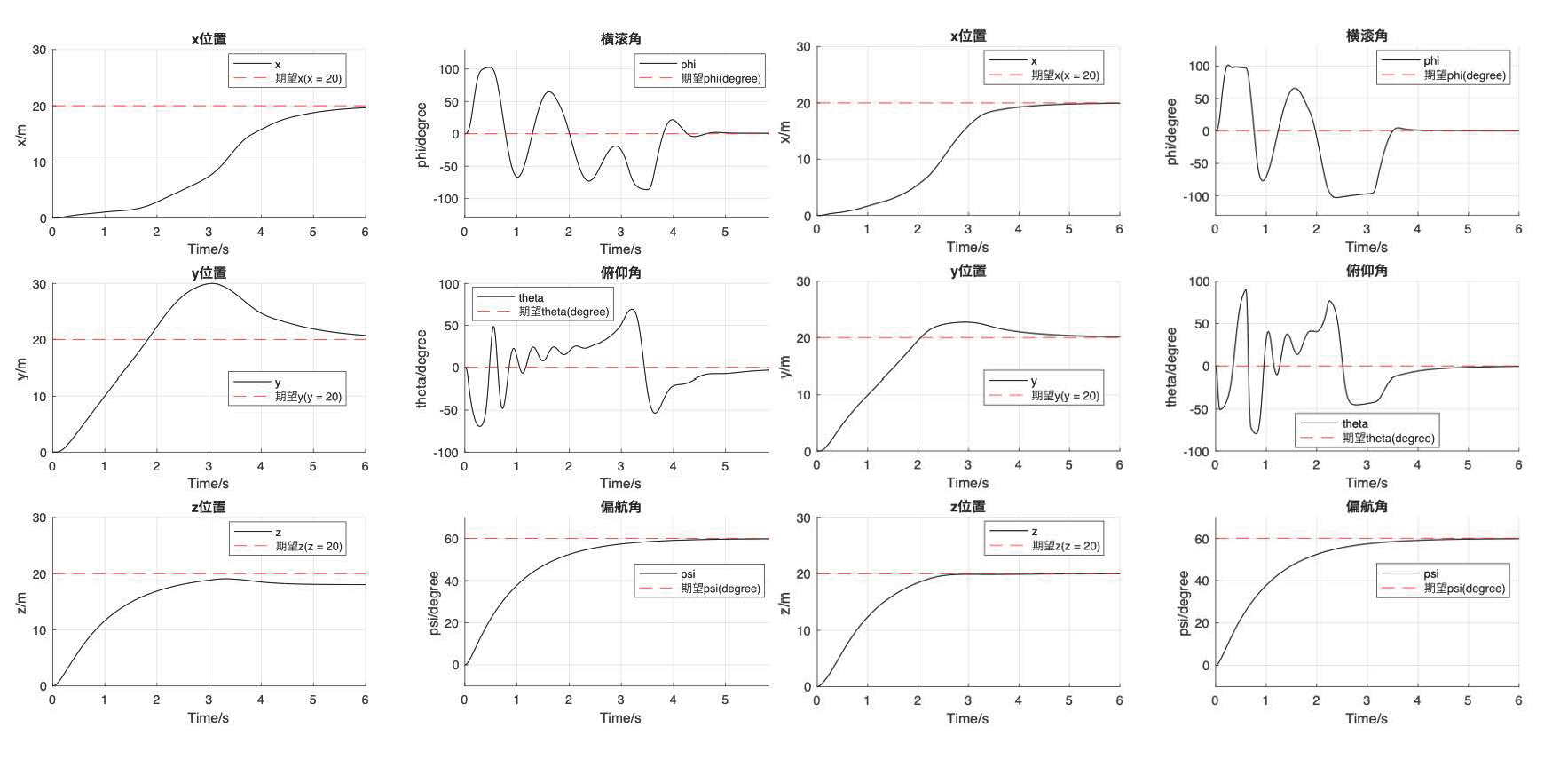
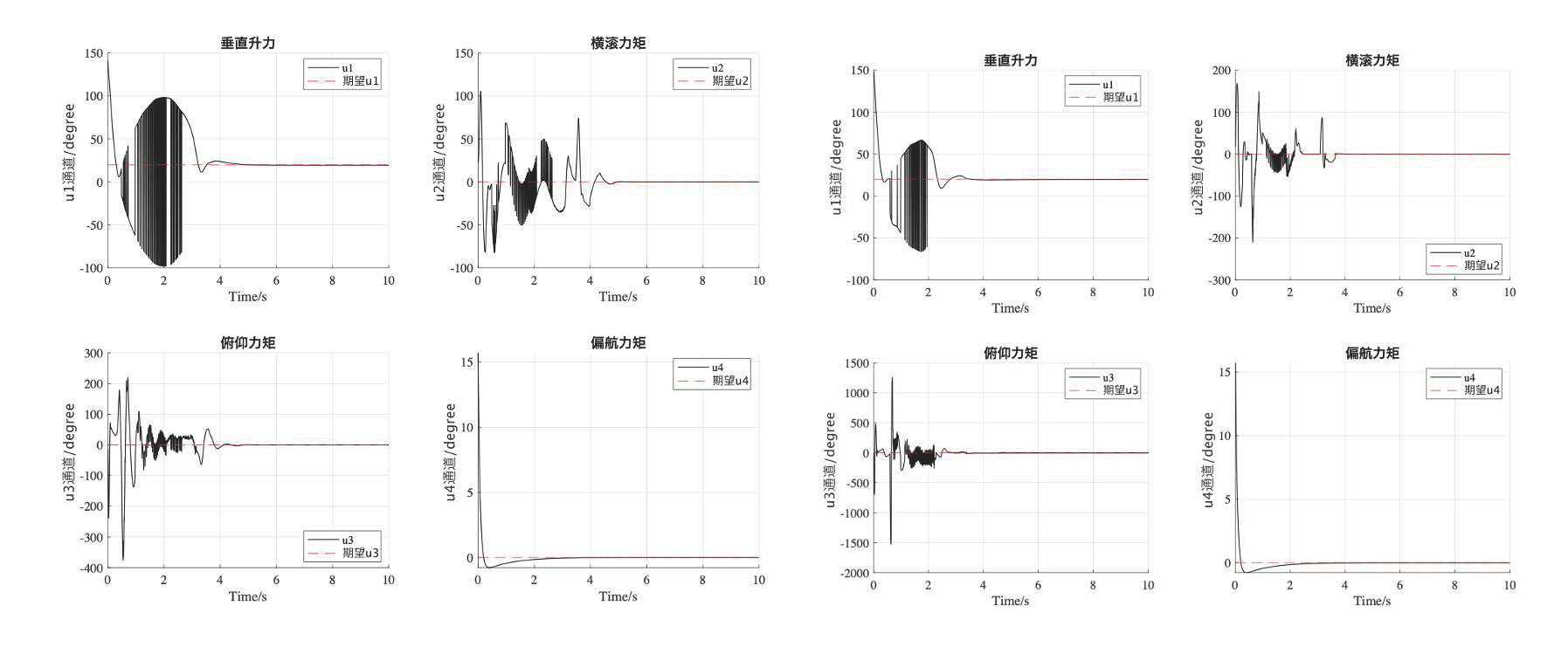
MATLAB Simulation Results Comparison

  • Position and Attitude Convergence Process: PD control vs. Feedforward PD control.
  • Four-channel Output Comparison: PD control vs. Feedforward PD control.

Design 2: A* Algorithm and Trajectory Optimization

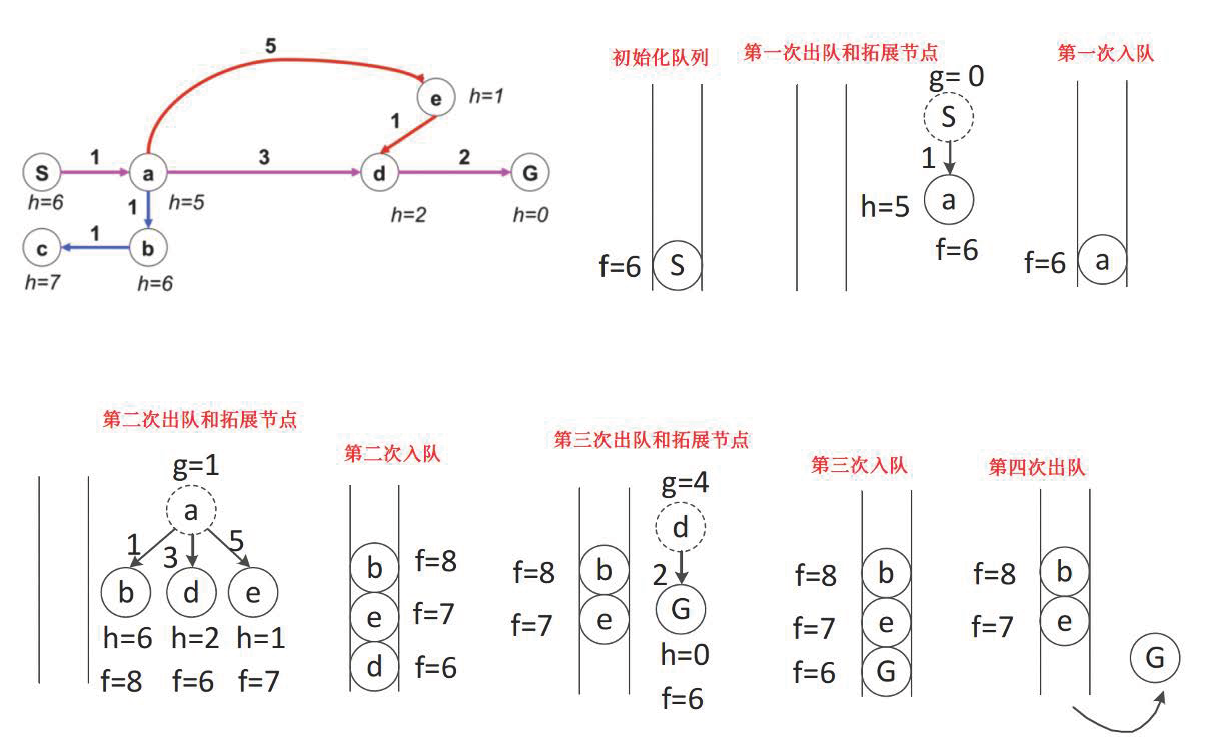
A* Algorithm

  • The A* algorithm incorporates a cost function \(f(n) = g(n) + h(n)\), where \(h(n)\) is the heuristic function.
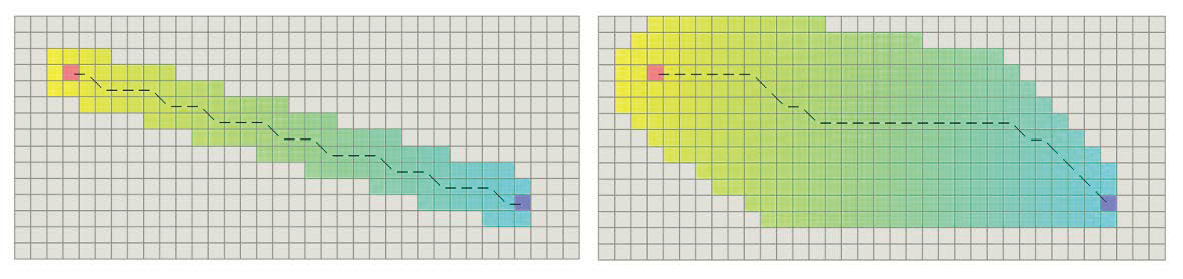
  • Heuristic Function Comparison: Diagonal distance heuristic vs. Euclidean distance heuristic.

Trajectory Optimization and B-Spline

  • Trajectory Optimization: This study considers various factors, such as position (x), velocity (v), acceleration (a), jerk, and snap, to optimize the UAV trajectory.
  • B-Spline Curve: The B-Spline formulation is given as:
\[C(t) = \sum_{i=0}^{n}N_{i,p}(t)Q_i\]

B-Spline curves improve over Bezier curves by enhancing local control and stability in trajectory generation.

EGO-Planner Algorithm Research

Algorithm Overview

  • EGO-Planner is based on rapid local trajectory optimization utilizing non-Euclidean distance fields.
  • ESDF (Euclidean Signed Distance Field) provides gradient information about obstacles but has certain limitations.

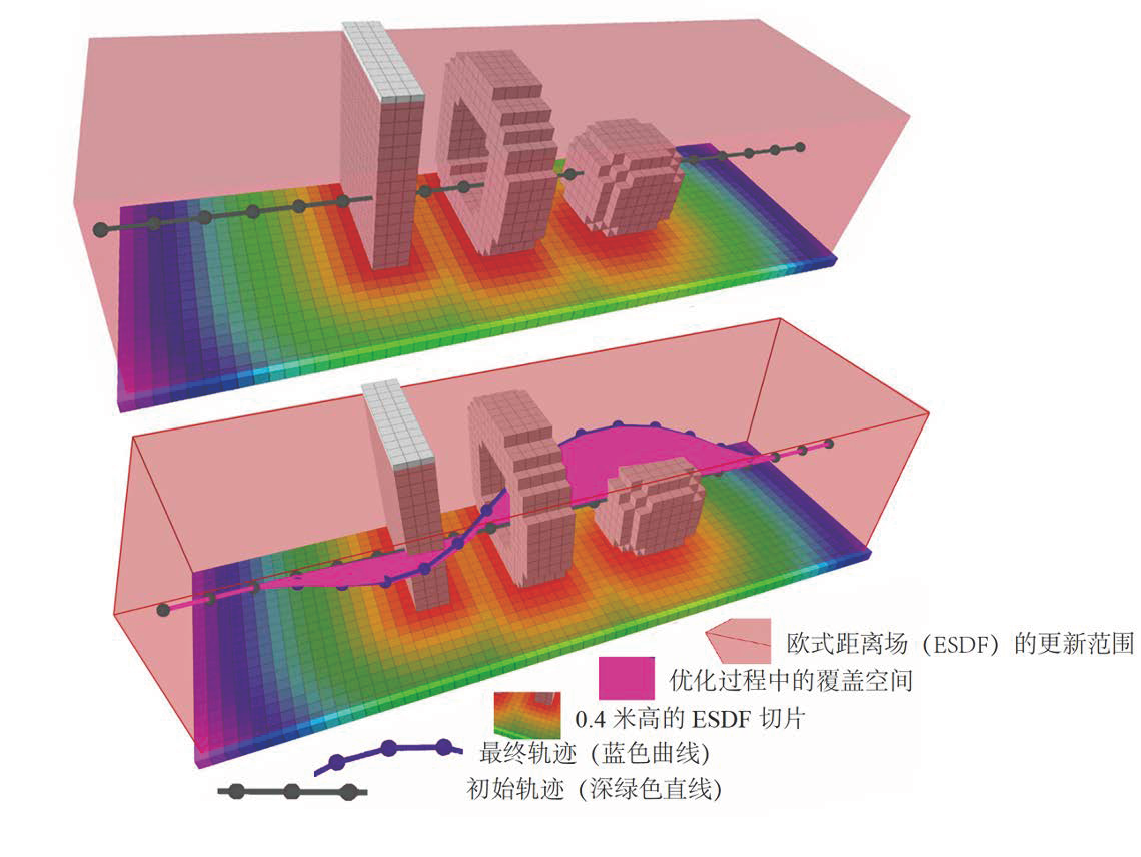
Optimization Problem

The optimization problem can be formulated as:

\[\min_{\mathbf{Q}}T = \lambda_sT_s + \lambda_cT_c + \lambda_dT_d\]
  • Smoothness Penalty Term:
\[T_s = \sum_{i=1}^{N_c-1}\parallel A_i \parallel_2^2 + \sum_{i=1}^{N_c-2}\parallel J_i \parallel_2^2\]
  • Collision Penalty Term:
\[T_c = \sum_{i=1}^{N_c}j_c(\mathbf{Q}_i)\]
  • Feasibility Penalty Term:
\[T_d = \sum_{i=1}^{N_c}w_vF(\mathbf{V}_i) + \sum_{i=1}^{N_c-1}w_aF(\mathbf{A}_i) + \sum_{i=1}^{N_c-2}w_jF(\mathbf{J}_i)\]

​ ​

Conclusion and Experimental Results

  • Simulation Environment: A comprehensive ROS, Gazebo, and Rviz-based simulation environment was employed to validate the performance of the EGO-Planner algorithm.

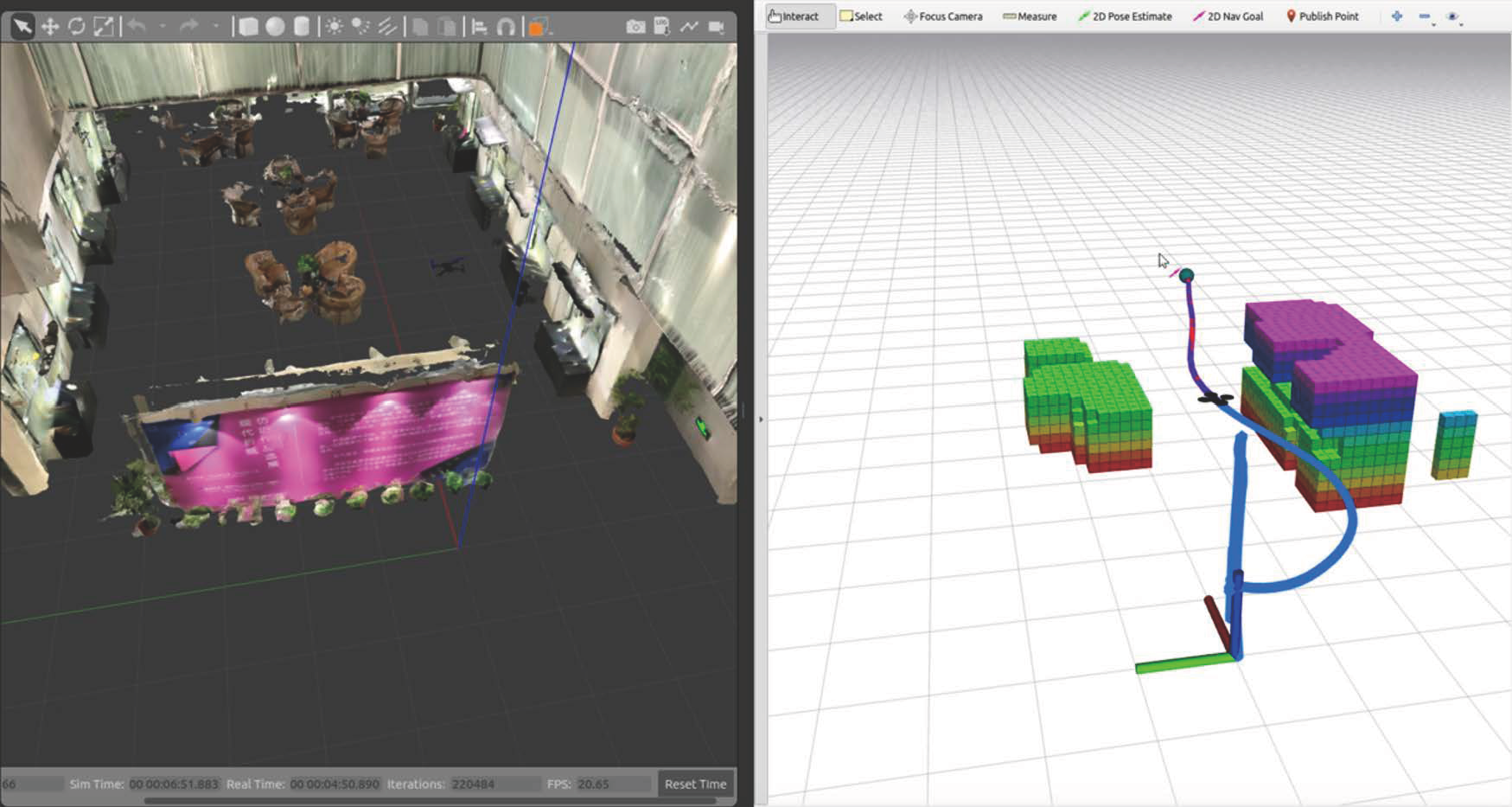
Experimental Conclusion

  • The EGO-Planner algorithm demonstrated superior performance in trajectory planning for quadrotor UAVs in complex indoor environments. Compared to traditional methods, it exhibited significantly faster planning speeds, allowing the UAV to quickly respond to dynamic environmental changes.
  • Additionally, the algorithm proved highly robust in obstacle avoidance, successfully preventing collisions in various test scenarios. This highlights the algorithm’s effectiveness in real-world applications where rapid and precise path adjustments are crucial.

Acknowledgments

Sincere thanks to my supervisor and the panel for their invaluable feedback and guidance.

References